ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ

Все оптические среды характеризуются абсолютным показателем преломления n, который называется показателем преломления. Абсолютным показателем преломления какой-либо оптической среды называется отношение синуса угла падения к синусу угла преломления при условии, что луч идет из вакуума в эту среду.

Показатель преломления вакуума, исходя из этого, равен единице. Обозначим угол падения луча через i, а угол преломления через i' Показатель преломления первой среды n, а второй n' тогда

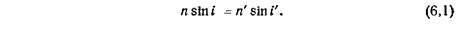Произведение показателя преломления среды на синус угла между нормалью и лучом при каждом преломлении есть величина постоянная, называемая оптическим инвариантом.

В геометрической оптике принимают показатель преломления воздуха также равным единице, хотя его точное значение n = 1,000274 (при нормальном давлении 760 мм рт. ст. и температуре 20°С).

Зависимость показателя преломления воздуха от температуры t°С и атмосферного давления определяется P_σ формулой

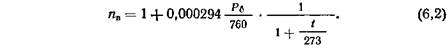Так. например, по этой формуле при P_σ=760 мм рт. ст. и t^oС=-50° п_в= 1,0003605. Часто для практических целей необходимо определять показатель преломления воздуха с точностью до 10^-6.

Показатель преломления оптических сред зависит от длины волны проходящего света, и его принято нормировать для линии натрия D, т. е. n_D. Обычно индекс D опускается. В ряде случаев, особенно в зарубежной практике, показатель преломления указывается для линии гелия d, т. е. n_d.

Показатели преломления для различных цветов в видимой области спектра приводятся в каталогах или ГОСТах на оптическое стекло, а для невидимой области спектра вычисляются на основе знания каких-либо трех показателей преломления для трех длин волн. Для этой цели служат так называемые дисперсионные формулы. При вычислении показателя преломления оптического стекла в инфракрасной области спектра для диапазона длин волн от 800 нм до 2600 нм хорошие результаты дает формула Неймана-Кетслера

Так, например, вычисление показателя преломления стекла марки ОФЗ λ=1,5 мкм для при известных n=1,59024 (λ=1,4 мкм), n=1,5850 (λ=1,7 мкм) и n=1,5792 (λ=2 мкм) дает значения:

с=0,00454462; b=-0,00483210; a =1,597392 и n_λ=1,58854

Пример 1. Луч идет из воздуха в плоскопараллельную пластинку под углом 30°. Пластинка имеет показатель преломления 1,5163. Определить угол преломления луча в пластинке.

Решение. Дано: i=30°; n= 1; n' =1,5163.

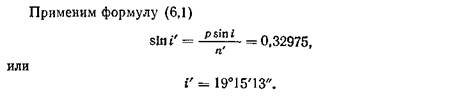Этот пример показывает порядок величин, необходимый для вычислений. В практике встречаются случаи, когда необходимо вычислять угол преломления с точностью до сотых долей секунды.