Товары не выбраны

ПРЕЛОМЛЕНИЕ ЛУЧЕЙ СФЕРИЧЕСКОЙ ПОВЕРХНОСТЬЮ

Сферическая поверхность О с радиусом кривизны r (рис. 9) разделяет две оптические среды с показателями преломления n и n'. Предмет расположен в точке А на расстоянии s от поверхности,

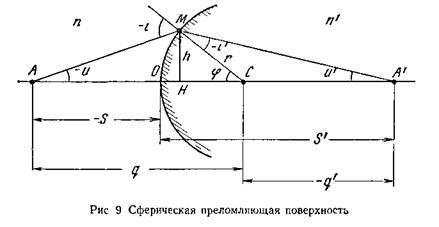а его изображение - в точке А' на расстоянии s' от той же поверхности. Луч света из точки А направляется на сферическую поверхность в точку М под конечным углом и. Луч падающий и луч преломленный с перпендикуляром МС образуют углы i и i'. Высота падения луча на поверхность h. Преломленный луч направляется в точку А' под углом и.

Обозначим расстояние от точек предмета А и изображения А' до центра кривизны С через q и q'.

Знаки величин указаны в соответствии с правилом знаков. Сферическая поверхность О разделяет два пространства - пространство предметов и пространство изображений.

Начальными данными для вычисления преломления луча на поверхности являются расстояние предмета от поверхности s' и угол u', под которым луч направляется на поверхность.

Для вычисления преломления луча необходимо знать значение кривизны поверхности и значения показателей преломления оптических сред, разделенных этой поверхностью

Искомыми данными являются положение изображения за поверхностью s' и угол u', под которым луч выходит из поверхности. Рассмотрим преломление действительного луча на одной сферической поверхности. Из рис. 9 следует

Формулы (13,1) - (13,6) являются основными для вычисления преломления луча на одной поверхности.

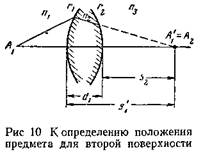Если оптическая система состоит из нескольких поверхностей, то необходимо последовательно выполнить аналогичные вычисления через все поверхности. При этом u₁'=u₂; u₂'=u₃ и т д Точка изображения после первой поверхности будет являться точкой предмета для второй поверхности и т. д. Рис. 10 поясняет переход с первой поверхности на вторую (здесь и в дальнейшем преломляющая поверхность обозначается индексом, характеризующим радиус кривизны этой поверхности). Легко видеть, что

В таком виде это уравнение называется уравнением нулевого луча.

Из уравнения (13,9) можем найти фокусные расстояния одной поверхности. Предположим, что луч идет на поверхность из бесконечности, тогда s=-∞, a s'=f'. Подставляя эти равенства в формулу (13,9), получим

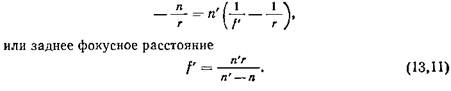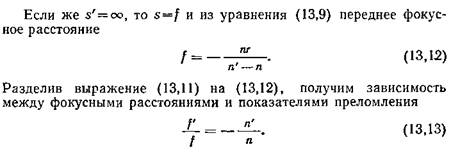Эту зависимость, найденную для одной поверхности, можно распространить и на систему, состоящую из ряда поверхностей.

В однородной среде фокусные расстояния оптической системы, переднее и заднее, равны по абсолютной величине и противоположны по знаку.

Если же первая и последняя оптические среды не одинаковы, что имеет место, например, если линза или объектив опущены в воду, то абсолютное значение фокусного расстояния зависит от величины радиуса кривизны первой поверхности. Отношение же переднего и заднего фокусных расстояний определяется уравнением (13,13).

Например в случае, когда линза с радиусами кривизны r₁= 17,58 и r₂=-21,03; d=5 и n=1,5467, имеющая фокусное расстояние /'=18,35 мм, опущена в воду так, что с водой (n=1,33) соприкасается поверхность с радиусом r₁, тогда f=-35,67 и f'=26,82 мм. Если же с водой соприкасается поверхность с радиусом r₂, то f=-32,95 и f'=24,77 мм. Также изменяется и местоположение изображения. В этих случаях отношение f'/f равно -1,33.

Вернемся к рис. 9 и установим зависимость между углами и и и' для нулевого луча. Эти углы в параксиальной области обозначим через α

Закон преломления напишем в виде

В таком виде эта формула, развернутая в схему, дает возможность наиболее просто производить вычисление прохождения нулевого луча через сложную оптическую систему.

Для вычисления хода луча, кроме того, необходимо знать формулу определения высоты h.

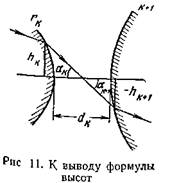Луч (рис. 11) падает на поверхность с радиусом кривизны r_k на высоте h_k, после преломления встречает поверхность с радиусом кривизны r_k+1 на высоте h_k+1. Расстояние между поверхностями d_k

Так как луч нулевой, то практически расстояние между вершиной поверхности и следом перпендикуляра (высоты) на оптической оси для каждой поверхности равно нулю.

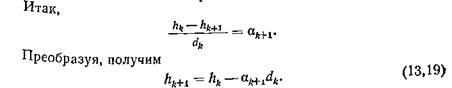Схема вычисления нулевого луча приведена в 41 (схема 3).

Пример 3. Определить местоположение щели спектрального прибора, освещаемого источником света с помощью конденсорной линзы, если расстояние от источника света до линзы равно 80 мм, а линза имеет конструктивные элементы r₁=40 мм, r₂= - 40 мм, d=5мм и n=1,5163.

Пример 4. Вычислить углы нулевого луча с оптической осью для случая, приведенного в примере 3.

Решение. Дано:

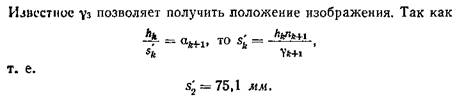Углы нулевого луча α найдутся путем деления соответствующего γ на показатель преломления: α₁= -0,5, α₂=0,01075, α₃=0,5319.

Обычно принято приводить α к последнему, равному 1, для чего необходимо все углы разделить на последний угол, т. е. получим окончательно α₁ = -0,94; α₂=0,0202; α₃=1.