ВЫЧИСЛЕНИЕ ДВУХЛИНЗОВОГО СКЛЕЕННОГО ОБЪЕКТИВА

Двухлинзовый склеенный объектив наиболее часто встречается во всевозможных оптических приборах. Простота конструкции, возможность коррегирования его на хроматическую и сферическую аберрации сделали его основным узлом различных оптических систем.

Каждый объектив характеризуется фокусным расстоянием (точнее, величиной заднего главного фокусного расстояния) и относительным отверстием. С конструктивной стороны объектив характеризуется диаметром, толщиной линз и радиусами кривизны. Толщина линз устанавливается в зависимости от диаметра объектива. Один из радиусов кривизны обеспечивает постоянство фокусного расстояния. Два других радиуса могут быть использованы как параметры для исправления аберраций. Таким образом, двухлинзовый склеенный объектив при заранее выбранной паре сортов оптического стекла как материала для деталей имеет два параметра для исправления аберраций. Этими двумя параметрами вместо радиусов для удобства вычислений являются углы нулевого луча с оптической осью. Оперируя двумя параметрами, можно исправить какие-нибудь две аберрации. Таковыми обычно являются сферическая аберрация для луча, идущего по краю отверстия объектива, и хроматическая разность сферических аберраций лучей спектра с длиной волны λ₁ и λ₂ (для видимой области спектра С и F), идущих в объектив на высоте, равной 0,7 высоты луча, идущего по краю отверстия.

Объектив (рис. 52) представляет собой комбинацию двух линз, склеенных между собой пихтовым бальзамом или бальзамином. Положительная линза - из крона, отрицательная - из флинта.

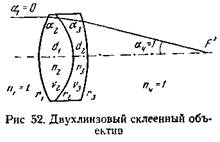С точки зрения коррекции комбинации "крон - флинт" или "флинт - крон", строго говоря, не тождественны, но практически особых преимуществ комбинация "флинт впереди" не имеет. Но так как крон в большинстве случаев значительно более устойчив против механических, атмосферных и других воздействий, то комбинация "крон впереди" получила всеобщее распространение.

Также надо сказать, что с точки зрения коррекции, данным условиям работы объектива (относительное отверстие, положение зрачка входа) соответствует определенная комбинация марок оптического стекла, которая позволяет получить лучшее выполнение условий синусов. Однако практически оказывается возможным ограничиться немногими комбинациями марок оптического стекла.

Из теории аберраций 3-го порядка известна формула хроматизма положения (f'=h₁; α₁=0; α'_m=1)

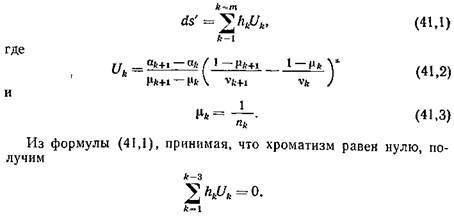Оптическую систему будем полагать тонкой, предмет расположен в бесконечности, предмет и изображение - в воздухе, а фокусное расстояние примем за единицу (f'=l). Так как d=0 и h₁=h₂=h₃=1, то хроматизм положения выражается уравнением

Следовательно, формулы (41,7) и (41,8) справедливы.

Эти формулы позволяют легко осуществить вычисление объектива тригонометрическим методом. Два параметра, Q и φ, позволяют исправить в объективе две аберрации. Коэффициент φ, зависящий от коэффициентов обратных относительных дисперсий (n'u), является параметром хроматической аберрации, a Q - сферической аберрации.

Методы вычисления двухлинзового склеенного объектива для видимой области спектра хорошо и подробно разработаны Г. Г. Слюсаревым.

Для других же областей спектра аналогичных разработок не имеется и выбор комбинации марок оптического стекла приходится делать на основании соображений об исправлении вторичного спектра.

Для объективов, предназначенных для работы в невидимой области спектра, обычно необходимо выполнить исправление сферохроматической аберрации, поэтому основным в расчете объектива является исправление хроматизма положения и сферической аберрации.

Вторичный спектр, как известно, в двухлинзовом склеенном объективе определяется формулой

где λ₀ - длина волны луча, принятая за основную, a λ₁ и λ₂ - длины волн, ограничивающих рассматриваемую область спектра.

Числитель последнего уравнения состоит из разностей частных относительных дисперсий, известных по каталожным данным. Поэтому выбор оптимальной комбинации марок оптического стекла может быть совершен заранее.

Однако следует предупредить, что выполнение условия ds=0 обычно приводит к значительной кривизне радиуса склейки, что делает невозможным исправление сферической аберрации, поэтому отыскивается компромиссное решение между исправлением вторичного спектра и исправлением сферической аберрации.

В некоторых случаях необходимо иметь заданный хроматизм положения: ds=C, тогда аберрационный параметр φ определяется выражением

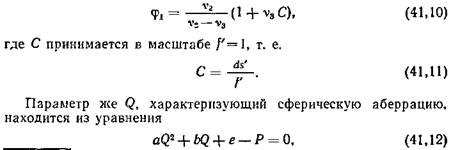Параметр же Q, характеризующий сферическую аберрацию, находится из уравнения

aQ² + bQ + e-P = 0,  (41,12)

Решение уравнения (41,12) дает два значения Q. Из этих значений принимаем Q меньшее по абсолютной величине. Если квадратное уравнение (41,12) не имеет решения, то экстремальное значение Q₀ находится путем его дифференцирования, т. е.

Если при найденных значениях φ₁ и Q сферическая аберрация велика, то она может быть уменьшена путем интерполирования по Q, а в случае оперирования с Q₀ — путем изменения пары марок оптического стекла.

Вычисление объектива покажем раздельно по операциям:

1. Выбор марок оптического стекла линз объектива. В качестве первой линзы рекомендуется принимать кроновое стекло как более устойчивое против атмосферных влияний.

Подбор комбинации пары марок стекла следует делать на основании их частных относительных дисперсий, стремясь получить их разность, близкую к нулю. Для объективов в ближней инфракрасной области (λ=0,8—2,4 мкм) рекомендуется пара стекол марок ФК4 и ОФЗ.

2. Установление толщин линз. Толщина положительной (первой) линзы устанавливается с тем расчетом, чтобы при данном диаметре D толщина по краю была не меньше величины d₀, указанной в табл. 2.

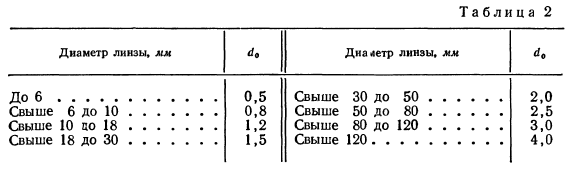
Тогда толщину по центру можно найти по формуле

округляя в сторону увеличения до целого числа.

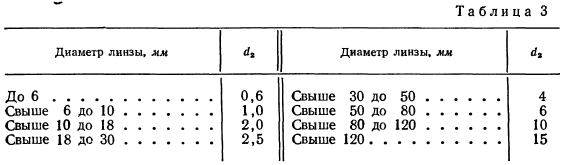
Толщина второй отрицательной линзы устанавливается с тем расчетом, чтобы при ее изготовлении не происходило «коробления» цвета поверхности, т. е. линза была бы достаточно прочна, не деформировалась. Для этого толщину отрицательной линзы в зависимости от ее диаметра рекомендуется брать из табл. 3.

3. Определение аберраций объектива. Вследствие сложности данного вопроса ограничимся здесь лишь общими соображениями.

Обычно выбирают величину сферической аберрации δ'_s для луча, падающего на объектив на высоте h_Kp=D/2, и хроматическую разность сферических аберраций ds'=0 для лучей спектра λ₁ и λ₂, идущих на высоте h_зона=0,7 h_кр.

В случае малосветосильных объективов с относительным отверстием не более 1 :6 рекомендуется иметь δs'=0. В случае более светосильных объективов δs' должна быть положительна и тем больше, чем больше относительное отверстие.

Таблица 4 дает представление о величинах продольной сферической аберрации, имеющейся у ряда объективов с большим относительным отверстием, для луча, идущего по краю объектива (для видимой области спектра).

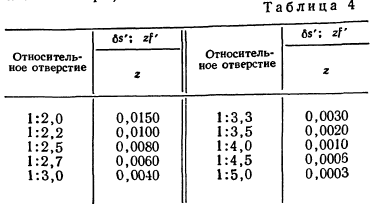
Если за объективом установлена призма (эквивалентная плоскопараллельной пластине), то ее аберрации следует учесть, принимая δs' и ds' отрицательными, так как аберрации призмы положительны. При этом сферическая аберрация призмы определяется по формуле

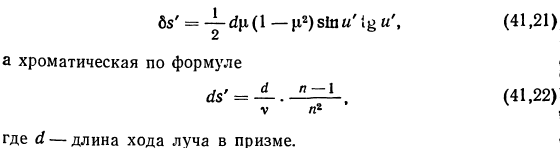
• 4. Определение h_кр и h_зона
  
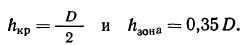
• 5. Вычисление С по формуле (41,11).
• 6. Определение φ₁ по формуле (41,10).
• 7. Вычисление а по формуле (41,13).
• 8. Вычисление b по формуле (41,14).
• 9. Вычисление е по формуле (41,15).
• 10. Определение Р по формуле (41,18).
• 11. Составление квадратного уравнения вида (41,12).
• 12. Решение квадратного уравнения, нахождение его кор­ней. В дальнейшем принимается Q меньше по абсолютной вели­чине.
• 13. Вычисление а₂ и а₃ по формулам
  
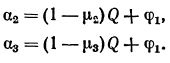
• 14. Вычисление высот для расчета радиусов:
  
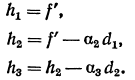
• 15. Вычисление радиусов по формуле
  
• 16. Вычисление нулевых лучей λ₀, λ₁ и λ₂ производится по схеме 3.
• 17. Вычисление крайних лучей λ₀, λ₁ и λ₂ производится по схеме 4 при h₁=h_кр и h₁=h_зона, причем показатели преломления берутся соответственно лучам λ₀, λ₁ и λ₂.
• 18. Составление таблицы аберраций.
• 19. Вычерчивание графика аберраций, подобно графику, приведенному на рис. 46.
• 20. Установление полного диаметра объектива. Полный диаметр линзы устанавливается в зависимости от способа крепления линз в оправе. Рекомендуется установить полный диаметр линзы по табл. 5, причем полученный из таблицы

диаметр следует увеличить до ближайшего нормального диаметра по ГОСТу (от 3 до 13 мм через 0,5 мм, далее до 48 мм через 1 мм и от 50 до 102 мм через 2 мм, в том числе 55, 65, 85 и 95 мм). На диаметры линз устанавливаются допуски, на положительную Л4, а на отрицательную Х3, кроме особых случаев (например, С3)