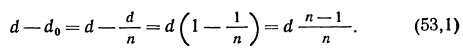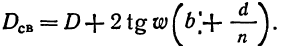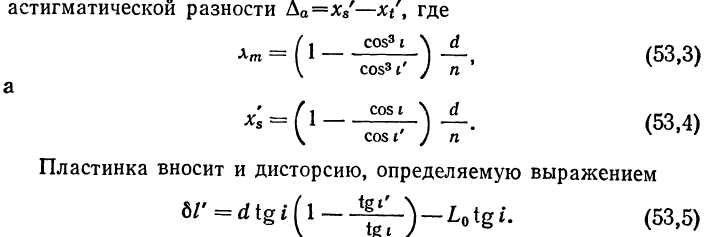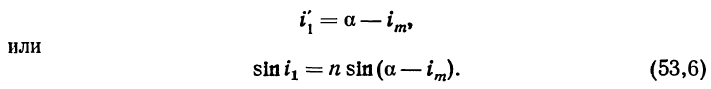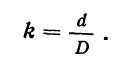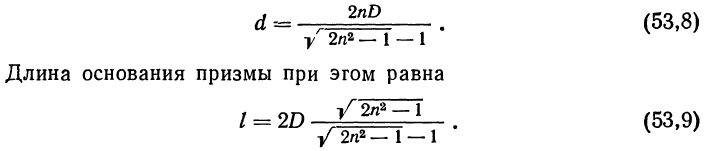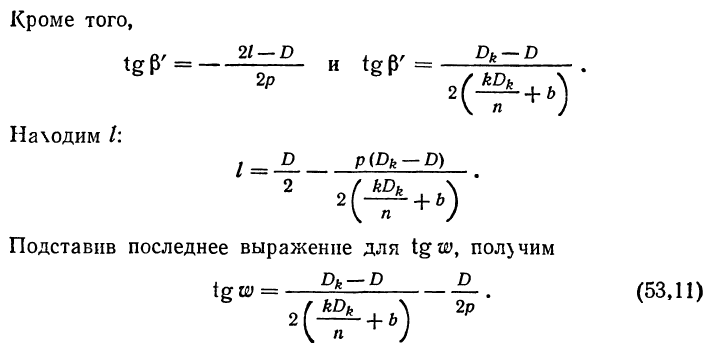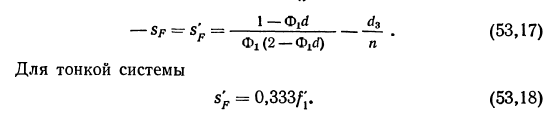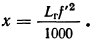ОПТИЧЕСКИЕ ДЕТАЛИ
Во многих оптических приборах различных конструкций применяются однотипные оптические детали в виде плоскопараллельных пластин, отражательных призм, объективов, коллективов и окуляров. Эти детали и узлы имеют определенные оптические свойства, которые не зависят от принципа устройства того или иного оптического прибора.
Плоскопараллельные пластины применяются в виде защитных, покровных, предметных, компенсационных стекол, светофильтров, сеток и зеркал. Оптический расчет их сводится к определению толщины и диаметра. Толщина пластины устанавливается из условий прочности или возможности изготовления точных полированных поверхностей. В последнем случае толщина пластины выбирается порядка 1/8—1/10 диаметра. При определении диаметра пластины необходимо учитывать преломление лучей внутри пластины, однако приемом редуцирования можно избежать определения величин углов преломления.
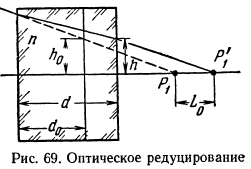
Редуцирование заключается в приведении оптической среды пластины к воздуху путем деления ее толщины на показатель преломления. Найдем разность действительной толщины и редуцированной:
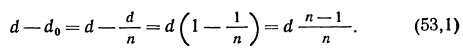
Это уравнение тождественно уравнению (17,2). Следовательно, в редуцированной пластине точка Р'1 (рис. 69) находится на том же месте, где она находилась бы в случае отсутствия пластины. Следовательно, можно рассматривать ход луча в редуцированной пластине без преломления, а так как
d — d0 = L0 то h0 = h.
При переходе от редуцированных пластин к действительным необходимо учитывать удлинение хода луча на величину смещения L0.
Редуцирование пластин упрощает расчет их диаметра если диаметр выходного (или входного) зрачка D, расстояние от пластины до зрачка b, толщина пластины d, показатель преломления n, а угол луча, выходящего из края зрачка и определяющего наибольший световой диаметр пластины с оптической осью w, то, применяя формулу высот (13,19), получим
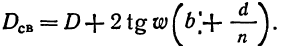
Так как толщина пластин обычно мала, то они вносят ничтожные аберрации Но в некоторых случаях их специально применяют для компенсации дисторсии, например в некоторых широкоугольных фотообъективах Толщина покровного стекла, применяемого в микроскопии (d=0,17 мм), также учитывается на аберрации при вычислении микрообъектива большого увеличения.
Астигматизм, вносимый плоскопараллельной пластинкой, установленной перед плоскостью изображения, определяется величиной
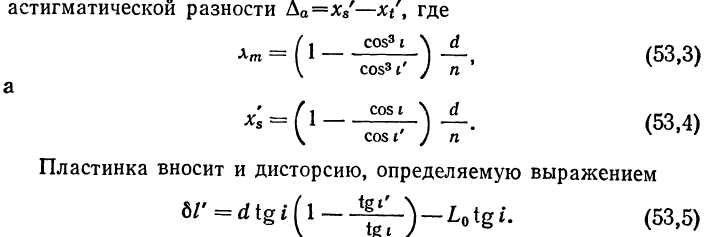
Если же пластины устанавливаются в параллельных пучках лучей, то они не влияют на аберрации.
Зеркала с внутренним серебрением также относятся к плоско-параллельным пластинам, поставленным под углом к оптической оси Лучи света в таких зеркалах дважды преломляются на входной поверхности.
Зеркала с наружным отражающим слоем также представляют собой плоскопараллельные пластины, но толщина их не влияет на ход лучей. Размеры таких зеркал определяются только по проекции светового пучка лучей на поверхности. Отражающим слоем обычно является алюминий, в связи с чем такие зеркала называются алюминированными. Такой слой значительно прочней серебряного.
Отражательные призмы. Если от одной или нескольких граней призмы происходит отражение пучков лучей, то такая призма называется отражательной.
Отражающие грани призм предназначены для полного отражения попадающих на них лучей. Если угол падения луча на отражающую грань меньше предельного угла полного внутреннего отражения im то такая грань должна быть посеребрена, что исключает возможность преломления на этой поверхности.
Для призм обычно выбирают сорта оптических стекол марок К8 с n= 1,5163 и БК10 с n =1,5688. Для этих сред имеем соответственно im =41°15'42" и
im =39°36'01".
Если на призму (рис. 70) падает луч перпендикулярно к входной поверхности, то отражающую поверхность он встречает под углом а.
В частном случае прямоугольной призмы а=45°, а так как этот угол больше предельного угла полного внутреннего отражения, луч отразится полностью вниз.
В общем случае, когда лучи идут к поверхности призм под углом ≠90°, может возникнуть опасность преломления на отражающей поверхности. Поэтому следует определить тот критический угол i1, начиная с которого происходит преломление на второй поверхности.
Из геометрических соотношений углов (рис. 70) получим
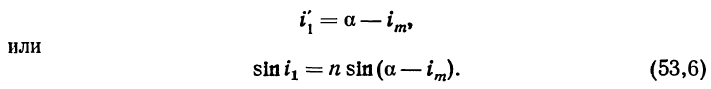
Для прямоугольной призмы (а=45°) из стекла сорта К8 i1=5°40'06", а из стекла БК10 i1 = 8°28'16".
Удвоенная величина этих углов дает представление об угловом поле зрения того участка оптического прибора, в котором размещена призма, которое не требует серебрения отражающей поверхности.
Отражательные призмы имеют значительное распространение в оптических приборах. Их основным назначением является: 1) изменение направления оптической оси в каком-либо месте прибора, 2) оборачивание изображения в заданном направлении.
Преломляющая призма может выполнить первое только в том случае, если изменение направления оптической оси мало (3—4°), так как в других случаях резкость изображения настолько ухудшается вследствие дисперсии, что пользование прибором становится практически невозможным. Кроме того, преломляющая призма вносит несимметричные аберрации относительно оптической оси, которые невозможно компенсировать линзовой оптикой. Отражательная призма может быть свободна от этого недостатка, но для этого она должна быть эквивалентна плоскопараллельной пластине. Для проверки этого условия призму развертывают в плоско-параллельную пластину, т. е. находят ее изображение относительно отражающей грани. Если отражающих граней несколько, то последовательно находят эти отражения от каждой грани.
Такая призма, будучи поставлена в прибор, вносит аберрации, равные аберрациям плоскопараллельной пластины. Но если призма расположена в параллельном пучке лучей, ее аберрации не оказывают практического действия на качество изображения всего прибора. Например, если призма расположена перед объективом зрительной трубы, при помощи которой рассматривают значительно удаленные предметы, то лучи различных длин волн, разложенные на составные части, по выходе из призмы идут параллельно друг другу и собираются объективом трубы в одну точку.
Другое дело, если призма расположена в сходящихся или расходящихся пучках лучей. Тогда она вносит аберрации, которые в большинстве случаев могут компенсироваться аберрациями линзовой части прибора.
Тип призмы определяется геометрической формой в главном сечении. Рассмотрим на примере прямоугольной призмы ее основное назначение и свойства (рис. 71). Как видно из рис. 71, а и 71, б, призма поворачивает оптическую ось на 90° и оборачивает изображение сверху вниз, т. е. в одном направлении. Развертка такой призмы показана на рис. 71, д. Призма развернулась в плоскопараллельную пластину с толщиной, равной длине хода луча в призме Длиня v луча в призме d является важной характеристикой любой отражающеи призмы.
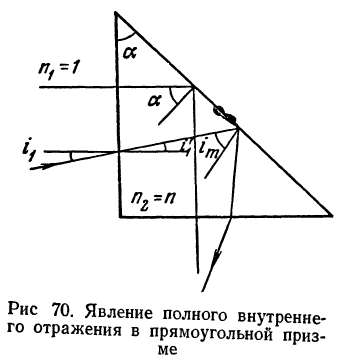
Отношение длины хода луча в призме к диаметру отверстия пучка лучей D назовем коэффициентом призмы k:
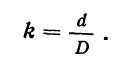
В прямоугольной призме катет определяет величину то отверстия, следовательно, коэффициент прямоугольной призмы равен единице.
Если лучи входят в призму со стороны гипотенузной поверхности (рис. 71,г), то пучок лучей изменяет направление на 180° и смещается. Изображение не оборачивается, так как первая отражающая грань поворачивает изображение, как и прямоугольная призма, сверху вниз, а вторая отражающая грань — снизу вверх. Развертка этой призмы показана на рис. 71, е. Длина хода луча d=2D т. е. k=2.
Если на прямоугольную призму падает луч под углом i1 (рис. 71, в), то выходящий из призмы луч не образует с входящим в нее лучом угол в 90°. Конструкции некоторых призм, из числа наиболее распространенных, показаны на рис. 72.
Прямоугольную призму (рис. 72, а) можно превратить в призму прямого зрения (призма Дове) (рис. 72 ,б). Такая призма оборачивает изображение сверху вниз, изменяя направление оптической оси только внутри призмы, сохраняя направление вошедшего и вышедшего лучей.
Так как луч, идущий по оптической оси, преломляется, то длина хода луча в призме зависит от показателя преломления и определяется по формуле
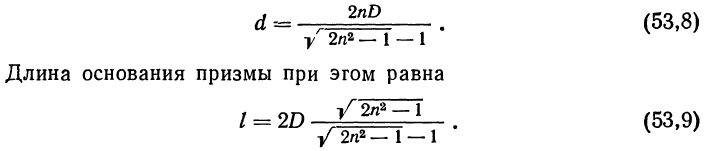
Для призмы из стекла К8 d=3,3812D и е = 4,2299 D, а для призмы из стекла БК10 d=3,2001 D и e=4,0398D.
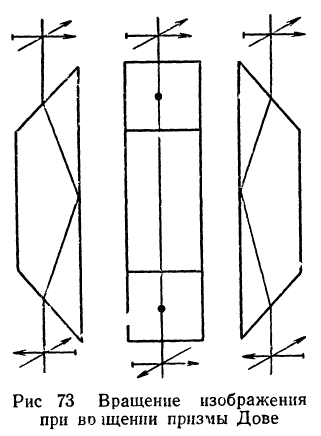
Призмой Дове (рис. 72, б) пользуются для того, чтобы вращать изображение (или компенсировать вращение изображения) в оптических приборах. Оптический механизм вращения показан на рис. 73. Изображение вращается со скоростью, вдвое большей скорости поворота самой призмы.
Недостатком этой призмы является то, что углы падения лучей на поверхности вверх и вниз от оптической оси несимметричны, а по абсолютной величине значительны (45° и более), что вызывает астигматизм, поэтому ее применяют только в плоскопараллельных пучках лучей.
Разновидностью семейства прямоугольных призм является призма-ромб (рис. 72,в), как бы состоящая из двух прямоугольных призм. Она не оборачивает изображения. Ход луча d=2D, K=2. Призма смещает лучи, оставляя направление входящего и выходящего лучей неизменным. Она находит себе частое применение в бинокулярных приборах для изменения глазного базиса. Верхняя ось может быть неподвижной, а нижняя качаться.
Пентапризма (рис. 72, г) поворачивает луч на 90° и не оборачивает изображения. Длина хода луча в ней d=3,4142 D, k=3,4142.
Свойством этой призмы является то, что луч, вышедший из призмы, с вошедшим лучом всегда сохраняет угол 90°. Этим обстоятельством пользуются в тех случаях, когда в измерительных целях необходимо строго сохранять между лучами угол 90°, например в дальномерах.
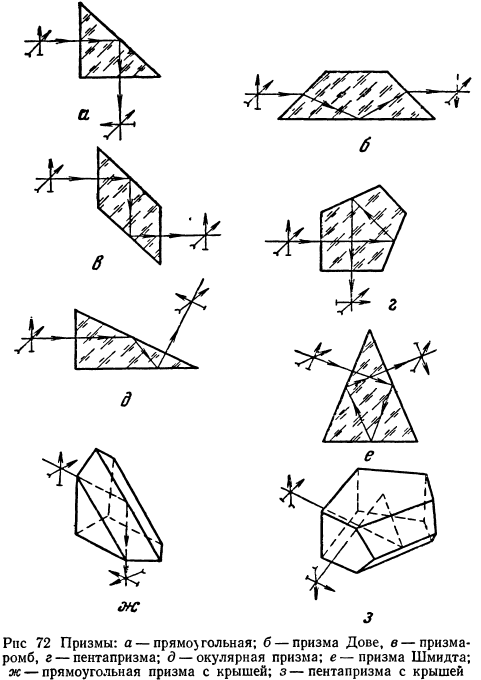
Половина пентапризмы позволяет образовать призму, называемую полупентапризмой (рис. 72, д). Она изменяет направление лучей на 45° и не оборачивает изображения. Длина хода луча в призме d=1,7071 D, или k=1,7071.
Призма нашла себе применение как окулярная призма, изменяющая направление оптической оси прибора на 45° и создающая удобное положение наблюдателю.
Особое место среди призм занимают крышеобразные призмы (дах призмы) (рис 72 ж, з). Любую отражающую призму можно превратить в крышеобразную, если одну из отражающих граней заменить двумя, составляющими между собой угол в 90°. Назначение крышеобразной призмы — повернуть изображение слева направо. Поэтому в оптическом приборе оправдывается появление только одной крышеобразной призмы.
Прямоугольная призма с крышей в главном сечении такая же, как обычная прямоугольная. Призма с крышей изменяет направление оптической оси на 90° и оборачивает изображение и сверху вниз и справа налево. Длина хода ее луча d= 1,732 Д или k= 1,732. Увеличение хода луча объясняется тем, что ширина призмы равна D, а высота должна быть больше, так как в том месте, где крыша на входной и выходной поверхностях образует угол, происходит срезание пучков лучей. Это обстоятельство следует иметь в виду для всех крышеобразных призм. Изготовление крыши на уже готовой обычной призме уменьшает световое отверстие. Крышеобразная пентапризма имеет k=5,031.
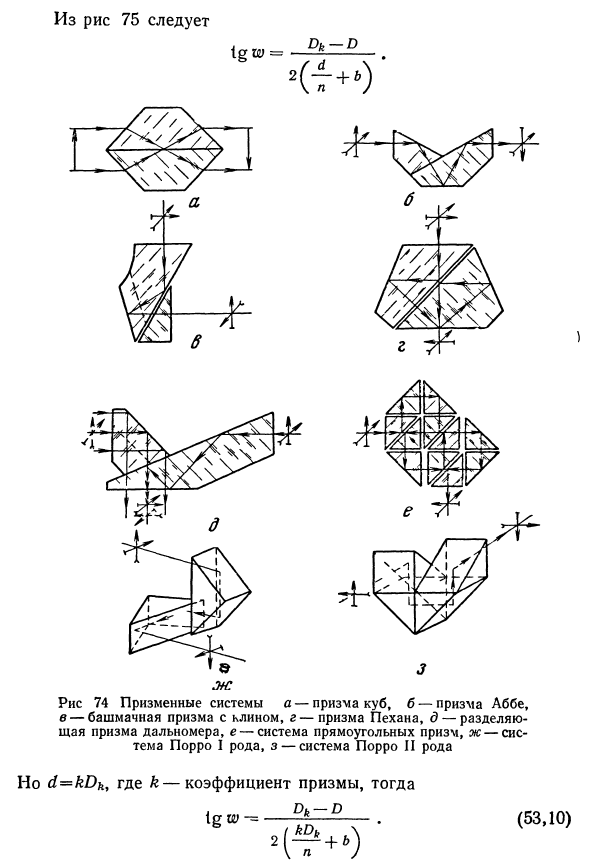
В оптических приборах находят себе применение комбинации различных призм, называемые призменными системами (рис 74) В современных призменных биноклях применяется система Малофеева, изобретенная им в 1827 г и известная под названием системы Порро I рода. Такая система из двух прямоугольных призм позволяет получить полное оборачивание изображения.
Установим зависимость между чистом отражающих граней и оборачиванием изображения. Если отражение пучков лучей происходит в одной плоскости, то нечетное число отражающих граней вызывает оборачивание изображения, а четное не вызывает. Последнее правило является недействительным, если отражение пучков лучей происходит в разных плоскостях.
Призмы ограничивают поле зрения оптических приборов Призма (рис 75) находится перед отверстием оптической системы на расстоянии b. Диаметр отверстия D. В отверстие поступает параллельный пучок лучей. Призма развернута в плоскопараллельную пластинку и редуцирована.
Например, прямоугольная призма с крышей, с отверстием Dk=70 мм из стекла К8 с п= 1,5163, расположенная перед оптической системой (объективом) со световым отверстием D=20 мм на расстоянии b=25 мм, пропускает в оптическую систему пучки лучей под углом w=18°5'.
Как видно из рис. 75, в систему проходят лучи и под большим углом, например лучи, показанные пунктиром, но их количество меньше, поэтому освещенность изображения, созданного этими лучами, уменьшена. Для практических целей выбирают отверстие D необходимое для работы, и вычисляют возможное поле зрения, исходя из полного заполнения светового отверстия лучами, идущими под углом w.

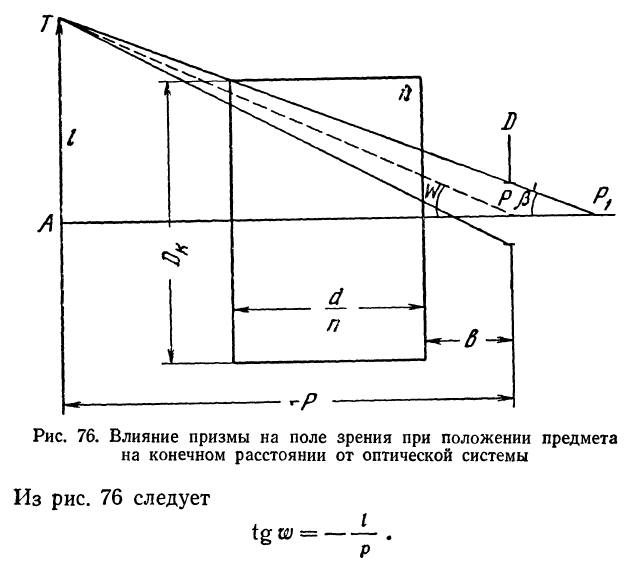
Рассмотрим влияние призмы на поле зрения в расходящихся пучках лучей (рис. 76). Угловое поле зрения таких систем определяется лучом, показанным пунктиром, направляющимся из края предмета Т в центр светового отверстия Р.
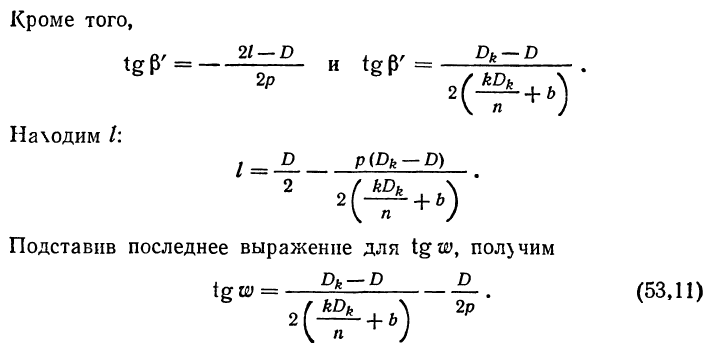
Для того же численного примера, при р=—600, имеем w=14°15'.
Призмы отрицательно влияют на поле зрения, уменьшая его с увеличением k.
Если отражательная призма, эквивалентная плоскопараллельной пластине, располагается в параллельном ходе лучей, то она не влияет на аберрации этой оптической системы, совместно с которой применяется. Но если она размещается в сходящихся или расходящихся пучках, то аберрации, вносимые ею, следует учитывать путем сложения с аберрациями того объектива, в ходе лучей которого она стоит.
Пример 23. Призма рефрактометра имеет показатель преломления n = 1,806. Определить показатель преломления испытуемого стекла, если измеренный угол полного внутреннего отражения равен 63°14'30".
Решение. Дано n= 1,806; im = 63o14'30".
Применим формулу
n'=n sin im= 1,6126.
Пример 24. В фотографический аппарат, применяемый для репродукции, введена прямоугольная призма с размером катета 70 мм из стекла с п= 1,5163. Определить астигматическую разность, вносимую призмой, для точек изображения, соответствующих полю зрения 2w = 40°.
Решение. Используем формулы (53,3) и (53,4), для которых углы преломления i' найдем по формуле (6,1), учитывая, что i1 = 20°:
sini'=sini / n = 0,22556,
i'=13°02'10'';cosi=0,97423. Так как d=70 мм, то x'm=4,74 мм и x's=1,64 мм, а следовательно,
Δa=x's-x'm=3,10 мм.
Объективом называется линза нли система линз оптического прибора, обращенная к предмету. Объектив характеризуется фокусным расстоянием относительным f ', отверстием и полем зрения 2w. В большинстве случаев объектив образует действительное изображение предмета.
Наиболее часто в различных оптических приборах применяется ахроматический двухлинзовый склеенный объектив (см. рис. 52). В некоторых случаях в геодезических и астрономических инструментах он применяется не склеенным.
Угловое поле зрения двухлинзовых объективов достигает 8—12°. Поэтому в тех случаях, когда необходимы более широкоугольные объективы, применяются конструкции фотографических многолинзовых объективов.
Если перед широкоугольным объективом необходимо разместить призмы, то в целях достижения их наименьшего размера необходимо призмы разместить во входном зрачке, а для этого входной зрачок должен быть расположен перед объективом (рис. 75) b = d/2n. Так как обычные или фотографические объективны, как правило, имеют входной зрачок внутри, то в качестве объективов применяют конструкции окуляров. При этом окуляры применяют повернутыми на 180° (в обратном ходе) против их обычного положения, чтобы их обычный выходной зрачок совпал со входным зрачком объектива.
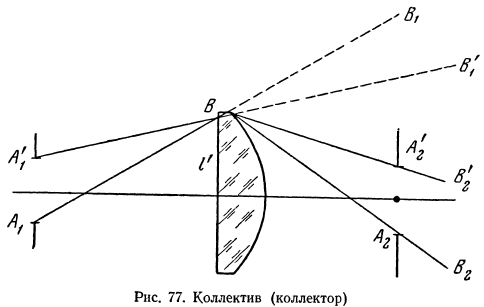
Коллективом, или коллектором, называется линза, устанавливаемая в плоскости действительного изображения или вблизи ее, назначение которой заключается в том, чтобы отклонить к оптической оси наклонные пучки лучей.
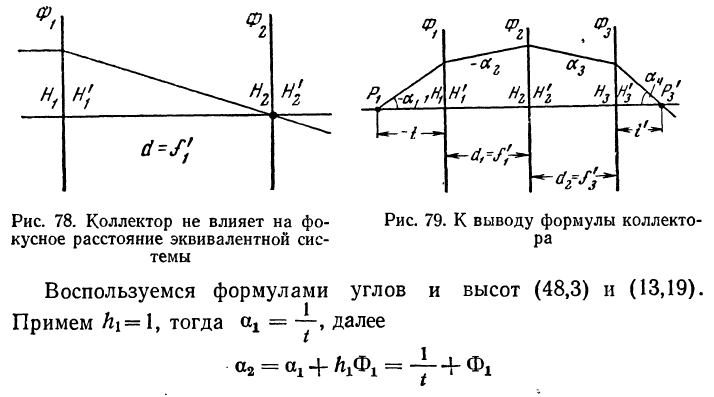
На рисунке 77 А1А'1 есть отверстие в первой оптической системе, из которого выходит пучок лучен А1ВА'1 в направлении В1В'1 показанном пунктиром. Если бы не было линзы, то лучи удалились бы от оптической оси и не смогли бы попасть в отверстие второй оптической системы А2А2. Лучи, вышедшие из точек А1 и А'1, пересекаются в точке В. Здесь находится изображение l'. Коллектив преломляет лучи и направляет их в отверстие А2А'2 по направлениям А2В2 И А'2В'2. Таким образом, коллектив проектирует выходной зрачок предшествующей оптической системы на входной зрачок последующей. Покажем, что линза, расположенная в плоскости изображения, не влияет на фокусное расстояние эквивалентной системы.
На рисунке 78 показаны две бесконечно тонкие системы Ф1 и Ф2, где Ф2 есть оптическая сила коллектива, установленного в фокальной плоскости первой системы Ф1.
По формуле оптической силы двух систем (49,5) имеем
Ф = Ф1 + Ф2 —f'Ф1Ф2,
где Ф2 = 1/f' тогда Ф = Ф2. Аналогичным образом можно рассмотреть и взаимодействие коллектива и второй системы А2А'2 (рис. 77).
Коллектив не влияет на ход пучка лучей, идущего из точки на сси оптической системы, а влияет на ход наклонных лучей.
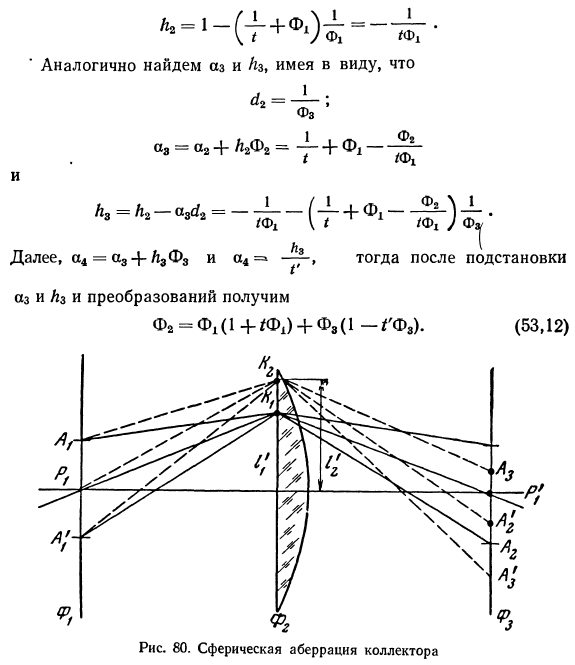
Найдем оптическую силу коллектива Ф2, расположенного в фокальной плоскости между двумя оптическими системами с оптическими силами Ф1 и Ф3 (рис. 79). Рассмотрим общий случай, когда луч выходит из точки Р1 перед первой системой, а по выходе из третьей системы пересекает оптическую ось в точке Р'3. Коллектив расположен в заднем фокусе первой оптической системы и в переднем фокусе второй.
Правильной работе коллектива мешает сферическая аберрация. При отсутствии сферической аберрации средние лучи Р1К1 и Р1К2 (рис.80) пересекали бы в пространстве изображений точку P'1. Оптическая сила коллектива выбрана таким образом, чтобы средний луч пучка лучей A1K1A'1 после преломления пересекал оптическую ось в центре отверстия Р'1. Вследствие сферической аберрации средний луч пучка А1К2А'1, являющийся главным лучом, пересекает это отверстие в точке А2. Поэтому часть пучка лучей из точки K2, а именно А2А'3 не пройдет далее. Сферическая аберрация коллектива влияет на распределение освещенности по полю изображения.
Если оптическая сила коллектива подобрана так, чтобы луч из точки К2 проходил через точку Р'1, то средний луч пучка из точки К1 пересекает оптическую ось правее точки Р1 и в этом случае задерживаются лучи в верхней части пучка, выходящего из точки K1.
Покажем действие сферической аберрации коллектива в виде плоско-выпуклой линзы с данными:
г1 = 100 мм
n1=1
d1 = 20 мм
n2 = 1,5187
r2 = ∞
n3 = 1
Фокусное расстояние коллектива 192,8 мм. Лучи выходят из точки Р1 на расстоянии 385,6 мм перед коллективом. Сферическая аберрация такой линзы, показанная ниже, вызывает сферическую аберрацию в зрачках.

Окуляр. Для того чтобы нормальный глаз человека мог рассмотреть изображение, образованное оптической системой, без напряжения аккомодации, необходимо, чтобы из системы лучи выходили в виде параллельных пучков. Эту роль выполняет последняя линзовая система прибора, называемая окуляром. При помощи окуляра глаз рассматривает изображение, образованное предшествующими окуляру частями оптической системы. Окуляр как бы выполняет роль лупы. Только через лупу рассматривают предметы непосредственно, а через окуляры — изображение предметов.
Окуляр характеризуется следующими величинами: 1) фокусным расстоянием f'; 2) видимым увеличением Г =250/f1; 3) полем
зрения 2w'; 4) диаметром выходного зрачка D' 5) положением выходного зрачка t'; 6) расстоянием от рассматриваемого предмета (изображения) до первой поверхности SF.
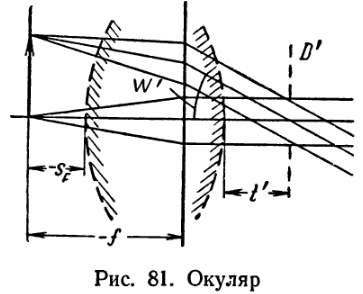
Принципиальная оптическая схема окуляра показана на рис. 81. Поверхности окуляра показаны пунктиром. Предмет расположен в плоскости изображений (передняя фокальная плоскость окуляра). Глаз наблюдателя устанавливается в центре выходного зрачка. Условие наблюдения требует достаточного удаления выходного зрачка от окуляра, чтобы все пучки лучей попали в зрачок глаза. Расстояние SF имеет значение в случае расположения сетки в передней фокальной плоскости окуляра или призмы между передней фокальной плоскостью и первой поверхностью окуляра. Для фокусировки на резкость изображения сетки необходимо изменять расстояние между сеткой и окуляром, а малое SF не позволяет разместить призму в этом пространстве.
Отметим, что с увеличением фокусного расстояния становится возможным применять более широкоугольные окуляры. Увеличению поля зрения окуляров препятствуют аберрации окуляра, в первую очередь астигматизм и кривизна поля. Если найти линейные аберрации, соответствующие одинаковым аберрациям в диоптриях при различных фокусных расстояниях, то окажется, например, что для меридиональной кривизны изображения Lm=3,6 и f'= 10 мм имеем угол поля зрения w' = 18°, а для f'=40—50 мм угол поля зрения w'=35°.
Простейшим окуляром может быть простая линза. Но она редко применяется без коллектива, роль которого была уже рассмотрена. Поэтому, как минимум, каждый окуляр состоит из двух линз. Первая линза со стороны передней фокальной плоскости окуляра называется коллективом, а со стороны глаза — глазной. Эти наименования сохранились и для более сложных окуляров.
В тех случаях, когда поле зрения не превосходит 2w'=30°, рекомендуется применять окуляры, состоящие из двух плосковыпуклых линз.
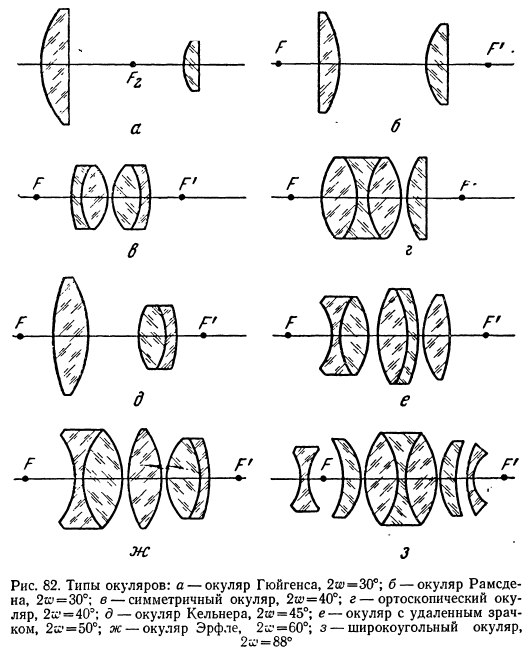
Наиболее распространенные конструкции окуляров показаны на рис. 82.
Окуляр Гюйгенса. Линзы плоской стороной обращены к наблюдателю, и плоскость изображения, образованная предыдущей системой, расположена между линзами. Такие окуляры обычно применяются в микроскопах. Их достоинством является сокращение длины системы, а недостатком — затруднения в установке сетки в фокальной плоскости. Вычисление конструктивных данных такого окуляра с фокусным расстоянием f рекомендуется производить с соблюдением следующих условий.
1. Для окуляров с увеличением не свыше 5х:
f'1 = 0,85f'; f'2 — 0,57f'; d = 0,92f'; стекло К9.
2. Для окуляров с увеличением не свыше 8х:
f'1 = 1,25f'; f'2 = 0,7f'; d = 1,05f', стекло Ф1.
3. Для окуляров с увеличением не свыше 15х:
f1' = 1,6f';f2' = 0,85f'; d= 1,15f'.
Стекла для окуляра 10х марок Ф1 и К9, а для 15х — ТФ1 и К9. Окуляр Рамсдена. Одинаковые плоско-выпуклые линзы обращены выпуклыми сторонами друг к другу. Применяя формулу оптической силы (49,5), при Ф1 = Ф2 имеем

Учитывая положение главной плоскости в плоско-выпуклой линзе с толщиной ds на расстоянии ds/n, окончательно получим
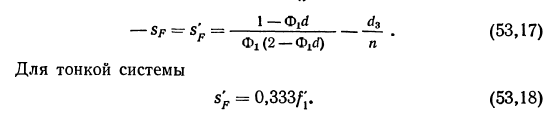
Окуляр в приборе обычно имеет некоторое перемещение (фокусировку) вдоль оптической оси с целью приспособления к недостаткам глаз наблюдателя в пределах до ±7 диоптрий (LT). Фокусировка окуляра позволяет близорукому или дальнозоркому глазу производить наблюдение без напряжения.
Для определения линейного перемещения окуляра, соответствующего тому или иному числу диоптрий, можно воспользоваться формулой (37,1), в которой под хт понимается линейное смещение х, а под Lm — число диоптрий LT. Тогда формула фокусировки окуляром примет вид
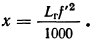
Для близорукого глаза окуляр вдвигается, а для дальнозоркого выдвигается.
Пример 25. Определить конструктивные элементы окуляра типа Рамсдена с видимым увеличением 10х.
Решение: Дано: Г, отсюда f' = 250/Г = 25 мм.
Применим формулы (53.16), (53,15):
f' = 1,5f' = 1,5*25 = 37,5 мм,
d2 = 0,5f'1 = 0,5*37,5 = 18,75 мм,
-SF = S'F = 10,52 мм.
Толщины и диаметры линз примем одинаковыми, хотя наибольший диаметр обычно должна иметь коллективная линза.
Диаметр линзы определяется полем зрения. Так как для окуляра типа Рамсдена 2w'=30°, то ожидаемый диаметр изображения в передней фокальной плоскости равен 2f'tgl5°, т. е. для данного случая 13,4 мм. Диаметр линзы обычно несколько больше
диаметра изображения. Примем световой диаметр линз 15 мм, а полный 16 мм. Толщина линзы найдется из графического построения кривизны поверхности из того расчета, чтобы толщина линзы по краю была 1—2 мм. Тогда d1=d2=3. Полученные конструктивные данные покажем в виде таблицы: