ВВЕДЕНИЕ В ВОЛНОВУЮ ТЕОРИЮ СВЕТА

Основные положения

Теория волнового движения представляет собой феноменологическую теорию, применимую с незначительными изменениями к широкой области звуковых и световых явлений, а также к волнам, распространяющимся по поверхности жидкости. При этом используется одна и та же система уравнений, так как названные явления имеют много общих черт и именно эти их общие черты описываются уравнениями волнового движения. При общем рассмотрении волновой теории и всех ее приложений, обсуждаемых в гл. 3—9, нет необходимости подробно определять физические свойства того вида возмущения, каковым является свет. Не имеет значения даже то, описывается ли рассматриваемое возмущение скалярной величиной, аналогичной, например, давлению газа, или величиной векторной, аналогичной напряженностям электрического и магнитного полей.

Теория волнового движения содержит три положения.

Существует некоторая физическая величина, которая в каждый момент времени имеет в каждой точке пространства определенное и измеримое значение.
Значение этой величины в какой-либо точке может с течением времени испытывать периодические изменения или возмущения.
Возмущение, существующее в некоторой точке пространства в данный момент времени, производит аналогичное возмущение в соседней точке в несколько более поздний момент времени, так что область возмущения непрерывно перемещается из одного места в другое.

Изучение волнового движения удобно начинать с простого гармонического осциллятора. Подобный осциллятор — это простейший и наиболее важный из многочисленных источников колебаний, которые могут создавать волны. Кроме того, движение такого осциллятора во многом схоже с движением точек среды, через которую проходят излучаемые им волны. Общую картину распространения волн можно описать с помощью сочетания уравнений простого гармонического движения с некоторыми общими уравнениями распространения возмущений.

Простой гармонический осциллятор

Незатухающий простой гармонический осциллятор является такой же математической абстракцией, как, например, блок без трения. Хотя совершенно незатухающий осциллятор не существует в природе, происходящие в нем процессы воспроизводят в первом приближении движения многих физических систем. С его помощью удается легко получить ряд важных результатов. В следующем приближении решения задачи о движении осциллятора нетрудно учесть эффекты затухания.

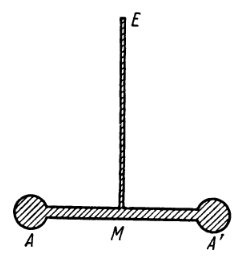
Рис. 2.1 Крутильный маятник.

При изучении простого гармонического осциллятора удобно иметь в виду некоторую определенную его модель. Поэтому мы начнем с рассмотрения крутильного маятника (рис. 2.1). Этот маятник состоит из двух равных масс А и А', связанных невесомым жестким стержнем. Стержень М в своей средней точке подвешен на тонкой проволоке, верхний конец Е которой неподвижно закреплен. Предположим, что данная система первоначально находилась в покое, затем стержень был повернут в горизонтальной плоскости на малый угол относительно вертикальной линии ЕМ и отпущен. Последующее движение системы можно изучать, рассматривая изменение величины q, которая определяется как линейное перемещение А (или А') от своего среднего положения. При этом подразумевается, что координата q измеряется по дуге горизонтальной окружности, вдоль которой перемещаются массы А и А'. Тогда

q = f(t), (2.1)

где t — время, отсчитываемое от какого-либо начального момента.

Экспериментальные данные

Наблюдая за движением маятника, можно установить следующее:

Маятник колеблется в горизонтальной плоскости. При этом промежуток времени между двумя моментами, в которые маятник проходит через положение равновесия, сохраняется постоянным. Интервал времени между двумя последовательными похождениями шаром А любой точки его траектории в одном и том же направлении называется периодом маятника.
Значение координаты q изменяется в пределах ± a. Величина а называется амплитудой колебаний В действительности амплитуда колебании постепенно уменьшается, однако при надлежащем выборе материала проволоки {ЕМ) уменьшение амплитуды за один период мало. Как указывалось выше, мы пока пренебрежем этим уменьшением амплитуды.

Рис. 2.2 Рис. 2.2. Зависимость смещения (а), скорости (б) и ускорения (в) от времени для гармонического осциллятора.

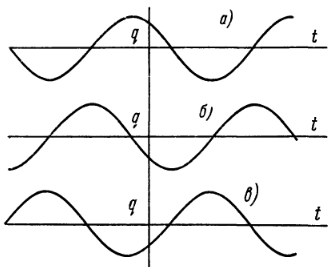
Зависимость q от t можно представить графиком, изображенным на рис. 2.2, а. Этот график описывается уравнением

q = a sin (ω t + δ) = a sin φ, (2.2)